4.6 Oxidation-Reduction Reactions
Learning Objectives
- Define oxidation and reduction.
- Identify redox reactions.
- Assign oxidation numbers to atoms in simple compounds.
- Recognise the oxidising agent and the reducing agent in a redox reaction.
- Balancing a redox reaction.
Consider this chemical reaction:
[latex]\ce{2Na}{(s)} + \ce{Cl_{2}}{(g)} → \ce{2NaCl}[/latex]
The reactants are elements, and it is assumed that they are electrically neutral; they have the same number of electrons as protons. The product, however, is ionic; it is composed of [latex]\ce{Na^{+}}[/latex] and [latex]\ce{Cl^{-}}[/latex] ions. Somehow, the individual sodium atoms as reactants had to lose an electron to make the [latex]\ce{Na^{+}}[/latex] ion, while the chlorine atoms as reactants had to each gain an electron to become the [latex]\ce{Cl^{-}}[/latex] ion. This reaction involves the transfer of electrons between atoms.
In reality, electrons are lost by some atoms and gained by other atoms simultaneously. However, mentally, we can separate the two processes. Oxidation is defined as the loss of one or more electrons by an atom (Figure 4.6.1). Reduction is defined as the gain of one or more electrons by an atom (Figure 4.6.1). In reality, oxidation and reduction always occur together; it is only mentally that we can separate them. Chemical reactions that involve the transfer of electrons are called oxidation-reduction (or redox) reactions.
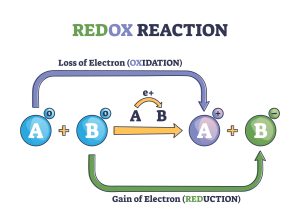
Oxidation Number
Redox reactions require that we keep track of the electrons assigned to each atom in a chemical reaction. How do we do that? We use an artificial count called the oxidation number to keep track of electrons in atoms. Oxidation numbers are assigned to atoms based on a series of rules. Oxidation numbers are not necessarily equal to the charge on the atom; we must keep the concepts of charge and oxidation numbers separate.
The rules for assigning oxidation numbers to atoms are as follows:
- The oxidation number of an atom as an element is zero. Examples: [latex]\ce{O}_{2},\ce{P}_{4},\ce{Fe},\ce{Br}_{2}[/latex] are the elemental forms at room temperature, and they all have an oxidation number of zero.
- The oxidation number of oxygen is usually [latex]-2[/latex] (except when bonded to [latex]\ce{F}[/latex]). Remember that in the element, oxygen [latex]\left(\ce{O}_{2}\right)[/latex] has an oxidation number of zero, whilst in peroxides [latex]\left(\ce{O}_{2}^{2-}\right)[/latex] each oxygen atom has an oxidation number of [latex]-1[/latex].
- The oxidation number of a monoatomic ion is equal to the ion’s charge. Examples: [latex]\ce{Na}^{+}=\ce{Na}\left(+1\right),\ce{Cl}^{-}=\ce{Cl}\left(-1\right),\ce{S}^{2-}=\ce{S}\left(-2\right)[/latex].
- The algebraic sum of the oxidation numbers in a neutral compound is zero; in a polyatomic ion, the sum of the oxidation number is equal to the ion’s overall charge.
- In combination of elements, the more electronegative element has its characteristic negative oxidation number (for example, [latex]\left(-3\right)[/latex] for nitrogen, [latex]\left(-2\right)[/latex] for oxygen, [latex]\left(-1\right)[/latex] for chlorine), and the more electropositive element has a positive oxidation number (for example, [latex]\left(+1\right)[/latex] for hydrogen, [latex]\left(+2\right)[/latex] for calcium, [latex]\left(+3\right)[/latex] for aluminium).
- The oxidation number of hydrogen is usually [latex]+1[/latex] due to its electronegativity being lower than that of the main-group elements to which it is normally bonded. With more electropositive elements, hydrogen has an oxidation number of [latex]\left(-1\right)[/latex] for instance, [latex]\ce{NaH}=\ce{Na}^{+}\ce{H}^{-}[/latex].
Example 4.6.1
Problems
Assign oxidation numbers to the atoms in each substance:
- [latex]\ce{Br_{2}}[/latex]
- [latex]\ce{SiO_{2}}[/latex]
- [latex]\ce{Ba(NO_{3})_{2}}[/latex]
Solutions
- [latex]\ce{Br_{2}}[/latex] is the elemental form of bromine. Therefore, by rule 1, each atom has an oxidation number of 0.
- By rule 2, oxygen is normally assigned an oxidation number of −2. For the sum of the oxidation numbers to equal the charge on the species (which is zero), the silicon atom is assigned an oxidation number of +4.
- The compound barium nitrate can be separated into two parts: the [latex]\ce{Ba^{2+}}[/latex] ion and the nitrate ion. Considering these separately, the [latex]\ce{Ba^{2+}}[/latex] ion has an oxidation number of +2 by rule 3. Now consider the [latex]\ce{NO_{3}^{-}}[/latex] ion. Oxygen is assigned an oxidation number of −2, and there are three oxygens. According to rule 4, the sum of the oxidation number on all atoms must equal the charge on the species, so we have the simple algebraic equation[latex]{x + 3(-2) = -1}[/latex], where [latex]{x}[/latex] is the oxidation number of the nitrogen atom and −1 represents the charge on the species. Evaluating,
[latex]\begin{array}{rrr} \\ x+(-6)&=&-1 \\ x&=&5 \end{array}[/latex]
Thus, the oxidation number on the [latex]\ce{N}[/latex] atom in the nitrate ion is +5.
Test Yourself
Assign oxidation numbers to the atoms in [latex]\ce{H_{3}PO_{4}}[/latex].
Answer
[latex]\ce{H} = +1, \ce{O} = −2, \ce{P} = +5[/latex]
All redox reactions occur with a simultaneous change in the oxidation numbers of some atoms. At least two elements must change their oxidation numbers. When the oxidation number of an atom is increased in the course of a redox reaction, that atom is being oxidised. When an oxidation number of an atom is decreased in the course of a redox reaction, that atom is being reduced. Oxidation and reduction are thus also defined in terms of increasing or decreasing oxidation numbers, respectively.
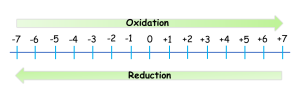
Example 4.6.2
Problem
Identify what is being oxidised and reduced in this redox equation:
[latex]\ce{2Na} + \ce{Cl_{2}} → \ce{2NaCl}[/latex]
Solution
Consider the reactants. Because both reactants are the elemental forms of their atoms, the [latex]\ce{Na}[/latex] and [latex]\ce{Cl}[/latex] atoms as reactants have oxidation numbers of 0. In the ionic product, the sodium ions have an oxidation number of [latex]+1[/latex], while the chloride ions have an oxidation number of [latex]−1[/latex], as shown below:
[latex]\begin{array}{rcrcrl} &\ce{2Na}&+&\ce{Cl2}&\rightarrow&\ce{2NaCl} \\ \text{ox}\#&0&&0&&+1-1 \end{array}[/latex]
We note that sodium is increasing its oxidation number from 0 to [latex]+1[/latex], so it is being oxidised; chlorine is decreasing its oxidation number from 0 to [latex]−1[/latex], so it is being reduced (Figure 4.6.3).
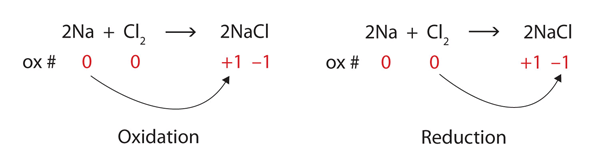
Because oxidation numbers are changing, this is a redox reaction. Note that the total number of electrons lost by the sodium (two, one lost from each atom) is gained by the chlorine atoms (two, one gained for each atom).
Test Yourself
Identify what is being oxidised and reduced in this redox equation:
[latex]\ce{C} + \ce{O_{2}} → \ce{CO_{2}}[/latex]
Answer
[latex]\ce{C}[/latex] is being oxidised from 0 to +4; O is being reduced from 0 to −2.
Oxidising Agents and Reducing Agents
Oxidising agents can oxidise another reactant by accepting electrons. Therefore, the oxidising agent becomes reduced (by gaining electrons) while oxidising another reactant (causing it to lose electrons).
Reducing agents reduce another reactant by offering electrons to the other reactant. Thus, the reducing agent becomes oxidised (by losing electrons) while reducing (gaining electrons) another reactant (causing it to gain electrons).
For instance, let’s consider the following reaction:
[latex]\ce{2Na} + \ce{Cl_{2}} → \ce{2NaCl}[/latex]
Here, sodium oxidised to become [latex]\ce{Na^{+}}[/latex] by donating an electron to chlorine, which causes chlorine to be reduced. Thus, sodium is the reducing agent in this reaction. Chlorine becomes chloride anion ([latex]\ce{Cl^{-}}[/latex]) by accepting an electron from sodium, which makes sodium to be oxidised. Therefore, chlorine is the oxidising agent in this reaction.
Balancing of Redox Equations
Redox equations are usually written as balanced net ionic equations, with spectator ions (ions that do not take part in the overall redox process) being omitted.
Determining the stoichiometry of a redox reaction can be challenging, even when the products of the reaction are known. For this reason, it is much more convenient and methodical to concentrate on the stoichiometry of each redox “half-reaction” or “redox couple” individually.
A five-step method for balancing redox equations, called the “half-reaction” method, is used, and after mastering these operations, any chemical redox equation can be balanced by combining these five steps.
- Divide the equation into the appropriate “half-reactions”, which can be balanced separately, for example:
Overall reaction \[
\ce{H}_{2}\ce{SO}_{3}+\ce{MnO}_{4}^{-}\rightarrow\ce{SO}_{4}^{2-}+\ce{Mn}^{2+}
\] Assign an oxidation number to each element in the ions or molecules of reactants and products:
Oxidation number of [latex]\ce{Mn}[/latex] in [latex]\ce{MnO}_{4}^{-}[/latex] is [latex]+7[/latex] and [latex]\ce{Mn}[/latex] oxidation number in [latex]\ce{Mn}^{2+}[/latex] is [latex]+2[/latex]
Thus, [latex]\ce{Mn}^{7+}[/latex] is being reduced to [latex]\ce{Mn}^{2+}[/latex].
So, the Reduction half-reaction is: \[
\ce{MnO}_{4}^{-}\rightarrow\ce{Mn}^{2+}
\] Oxidation number of [latex]\ce{S}[/latex] in [latex]\ce{H}_{2}\ce{SO}_{3}[/latex] is [latex]+4[/latex], and oxidation number of [latex]\ce{S}[/latex] in [latex]\ce{SO}_{4}^{2-}[/latex] ion is [latex]+6[/latex]
So, [latex]\ce{S}[/latex] is being oxidised from [latex]+4\rightarrow+6[/latex].
So, the oxidation half-reaction is: \[
\ce{H}_{2}\ce{SO}_{3}\rightarrow\ce{SO}_{4}^{2-}
\] - Write a separate balanced chemical equation for each redox-active species. This is the mass balance step:Add water to balance oxygen:
\[
\ce{MnO}_{4}^{-}+8\ce{H}^{+}\rightleftarrows\ce{Mn}^{2+}+4\ce{H}_{2}\ce{O}
\] Add [latex]\ce{H}^{+}[/latex] to balance hydrogens: \[
\ce{H}_{2}\ce{SO}_{3}+\ce{H}_{2}\ce{O}\rightleftarrows\ce{SO}_{4}^{2-}+4\ce{H}^{+}
\] - Although we have now achieved mass balance, we also need to balance the charge by adding electrons (negative charge) as needed. This generates the balanced electrochemical half-reaction. The total charge on each side of a balanced reaction must be the same: \[
\ce{MnO}_{4}^{-}+8\ce{H}^{+}+5e\rightleftarrows\ce{Mn}^{2+}+4\ce{H}_{2}\ce{O}
\] Left-hand side (LHS) total charge [latex]+2[/latex]
Right-hand side (RHS) total charge [latex]+2[/latex]
And: \[
\ce{H}_{2}\ce{SO}_{3}+\ce{H}_{2}\ce{O}\rightleftarrows\ce{SO}_{4}^{2-}+4\ce{H}^{+}+2e
\] LHS total charge [latex]0[/latex]
RHS total charge [latex]0[/latex]
If all three steps have been done correctly, one half-reaction will have electrons on the left-hand side of the equation (the reduction half-reaction), while the other half-reaction will have electrons on the right-hand side of the equation (the oxidation half-reaction). - The balanced half-reactions can be termed ‘electrochemical equations’ since they involve the electrons. To obtain a chemical equation for the reaction, we need to eliminate the electrons from the overall equation. Hence, the fourth step is the addition of the two half-reactions in such a way that the electrons cancel out. This may require multiplying one equation or both by an appropriate integer.
For the two half-reactions above:
\[\begin{align*}
2 & \left\{ 5e+8\ce{H}^{+}\ce{MnO}_{4}^{-}\rightleftarrows\ce{Mn}^{2+}+4\ce{H}_{2}\ce{O}\right\} \\
5 & \left\{ \ce{H}_{2}\ce{SO}_{3}+\ce{H}_{2}\ce{O}\rightleftarrows\ce{SO}_{4}^{2-}+4\ce{H}^{+}+2e\right\}
\end{align*}\] The first reaction is multiplied by two, and the second reaction is multiplied by five, and both are added to give: \[
5\ce{H}_{2}\ce{SO}_{3}+2\ce{MnO}_{4}^{-}+16\ce{H}^{+}+5\ce{H}_{2}\ce{O}+10e\rightleftarrows2\ce{Mn}^{2+}+5\ce{SO}_{4}^{2-}+20\ce{H}^{+}+8\ce{H}_{2}\ce{O}+10e
\] Note the equal number of electrons on each side of the equation cancel out. - The final step is to cancel the electrons and simplify the chemical equation by eliminating any chemical species common to each side of the equation.
As shown in Table 4.6.1, balance the [latex]\ce{H^{+}}[/latex] ions and [latex]\ce{H_{2}O}[/latex] molecules on each side.
Table 4.6.1: Number of atoms of elements on each side of the equation.
| LHS | RHS | Balance |
|---|---|---|
| [latex]16\ce{H}^{+}[/latex] | [latex]20\ce{H}^{+}[/latex] | [latex]20-16=4\ce{H}^{+}[/latex] on RHS |
| [latex]5\ce{H}_{2}\ce{O}[/latex] | [latex]8\ce{H}_{2}\ce{O}[/latex] | [latex]8-5=3\ce{H}_{2}\ce{O}[/latex] on RHS |
\[
5\ce{H}_{2}\ce{SO}_{3}+2\ce{MnO}_{4}^{-}\rightleftarrows2\ce{Mn}^{2+}+5\ce{SO}_{4}^{2-}+3\ce{H}_{2}\ce{O}+\ce{4H}^{+}
\]
Examples 4.6.3
Test Yourself
Balance the following redox equation:
[latex]\ce{H}^{+}+\ce{Al}\rightarrow\ce{Al}^{3+}+\ce{H}_{2}[/latex]
Answer
Step 1 – Divide the equation into the appropriate “half-reactions” which can be balanced separately.
Reduction half-reaction:
[latex]\ce{H}^{+}\rightarrow\ce{H}_{2}[/latex]
Oxidation half-reaction:
[latex]\ce{Al}\rightarrow\ce{Al}^{3+}[/latex]
Step 2 – Write a separate balanced chemical equation for each redox-active species. This is the mass balance step.
Reduction half-reaction:
[latex]\ce{2H}^{+}\rightarrow\ce{H}_{2}[/latex]
Oxidation half-reaction:
[latex]\ce{Al}\rightarrow\ce{Al}^{3+}[/latex]
Step 3 – Balance the net charge of each half-reaction by adding electrons.
Reduction half-reaction:
[latex]\ce{2H}^{+}+2e\rightarrow\ce{H}_{2}[/latex]
Oxidation half-reaction:
[latex]\ce{Al}\rightarrow\ce{Al}^{3+}+3e[/latex]
Step 4 – Add two half-reactions in such a way that the electrons cancel out. Multiply the reduction half-reaction by three and the oxidation half-reaction by two to get an equal number of electrons on both sides.
Reduction half-reaction:
[latex]3 \left(2\ce{H}^{+}+2e\rightarrow\ce{H}_{2}\right)[/latex]
[latex]6\ce{H}^{+} +6e\rightarrow3\ce{H}_{2}[/latex]
Oxidation half-reaction:
[latex]2 \left(\ce{Al}\rightarrow\ce{Al}^{3+}+3e\right)[/latex]
[latex]2\ce{Al} \rightarrow2\ce{Al}^{3+}+6e[/latex]
Add two reactions:
[latex]6\ce{H}^{+}+6e+2\ce{Al} \rightarrow3\ce{H}_{2}+2\ce{Al}^{3+}+6e[/latex]
Step 5 – Cancel the electrons and simplify the chemical equation by eliminating any chemical species common to each side of the equation as follows:
[latex]6\ce{H}^{+}+2\ce{Al}\rightarrow3\ce{H}_{2}+2\ce{Al}^{3+}[/latex]
Batteries
Redox reactions have a wide range of applications across science, industry, and technology. From powering our electronic devices to enabling critical biological processes and environmental cleanup, these reactions are integral to our everyday lives and the advancement of various fields. One of the most well-known applications of redox reactions is in batteries (Figure 4.6.4).

Redox reactions play a critical role in the functioning of batteries as they consist of two electrodes, an anode and a cathode, separated by an electrolyte. When the battery is discharging, a chemical reaction occurs at the anode (oxidation) and another at the cathode (reduction). Electrons flow from the anode to the cathode through an external circuit, creating an electric current. This flow of electrons is what powers our devices and vehicles. The overall reaction in a battery is a redox reaction, and the specific reactions depend on the type of battery (e.g. alkaline, lithium-ion, lead-acid).
For instance, the primary redox reaction that occurs in an alkaline battery involves the following key components:
- Anode (Negative Electrode)
The anode typically consists of powdered zinc ([latex]\ce{Zn}[/latex]) and a gel-like mixture of zinc and potassium hydroxide ([latex]\ce{KOH}[/latex]). The zinc metal serves as the active material in the anode.
The redox reaction at the anode is the oxidation of zinc:
[latex]\ce{Zn}{(s)} → \ce{Zn^{2+}}{(aq)} + {2e^{-}}[/latex]
As zinc atoms lose electrons, they are oxidised into zinc ions ([latex]\ce{Zn^{2+}}[/latex]), releasing two electrons in the process. [latex]\ce{Zn^{2+}}[/latex] then reacts with hydroxyl ions in the electrolyte solution to form zinc hydroxide.
The overall reaction at the anode is:
[latex]\ce{Zn}{(s)} + \ce{2OH^{-}}{(aq)} {\rightarrow} \ce{Zn(OH)_{2}}{(s)} + {2e^{-}}[/latex]
- Cathode (Positive Electrode)
The cathode is usually composed of manganese dioxide ([latex]\ce{MnO_{2}}[/latex]) and a mixture of graphite.
The redox reaction at the cathode is the reduction of manganese dioxide:
[latex]\ce{2MnO_{2}}{(s)} + \ce{2H_{2}O}{(l)} + {2e^{-}} → \ce{2Mn_{2}O_{3}}{(s)} + \ce{2OH^{-}}{(aq)}[/latex]
The overall redox reaction in an alkaline battery is:
[latex]\ce{Zn}{(s)} + \ce{2MnO_{2}}{(s)} ⇌ \ce{Mn_{2}O_{3}}{(s)} + \ce{ZnO}{(aq)}[/latex].
Key Takeaways
- Oxidation-reduction (redox) reactions involve the transfer of electrons from one atom to another.
- Oxidation numbers are used to keep track of electrons in atoms.
- There are rules for assigning oxidation numbers to atoms.
- Oxidation is an increase in oxidation number (a loss of electrons); reduction is a decrease in oxidation number (a gain of electrons).
- An oxidising agent causes the oxidation of another reactant by accepting electrons, and a reducing agent causes the reduction of another reactant by donating electrons.
- Redox equations can be balanced using the half-reaction method.
Exercises
Media Attributions
- Redox reaction as atoms chemical oxidation states change outline diagram. Labeled educational explanation scheme with electron gain and loss in oxidation or reduction process vector illustration. © VectorMine-stock.adobe.com
- Set of metal batteries, accumulators, button cells, power bank of different sizes. Nickel and lithium energy sources for electric devices. Colored flat vector illustration isolated on white background © Good Studio-stock.adobe.com
An ion composed of more than one atom. For example nitrate ion, phosphate ion and sulphate ion. Nitrate ion is composed of one nitrogen and three oxygen atoms.
The relating of one chemical substance to another using a balanced chemical reaction.

