1.4 Temperature and Density
Learning Objectives
- Learn about the various temperature scales that are commonly used in chemistry.
- Define density and use it as a conversion factor.
Temperature
One of the fundamental quantities in science is temperature. Temperature is a measure of the average amount of energy of motion, or kinetic energy [1], a system contains. Temperatures are expressed using scales that use units called degrees, and there are several temperature scales in use. One of the commonly used temperature scales is the Fahrenheit scale (symbolised by °F and spoken as “degrees Fahrenheit”). On this scale, the freezing point of liquid water (the temperature at which liquid water turns to solid ice) is 32°F, and the boiling point of water (the temperature at which liquid water turns to steam) is 212°F.
Science also uses other scales to express temperature. The Celsius scale (symbolised by °C and spoken as “degrees Celsius”) is a temperature scale where 0°C is the freezing point of water and 100°C is the boiling point of water; the scale is divided into 100 divisions between these two landmarks and extended higher and lower. By comparing the Fahrenheit and Celsius scales, a conversion between the two scales can be determined as follows:
[latex]\begin{array}{rllll} ^{\circ}\text{C}&=&(^{\circ}\text{F}-32)&\times &\dfrac{5}{9} \\ \\ ^{\circ}\text{F}&=&\left(^{\circ}\text{C}\times \dfrac{9}{5}\right)&+&32 \end{array}[/latex]
Using these formulas, we can convert from one temperature scale to another. The number 32 in the formulas is exact and does not count in significant figure determination.
Example 1.4.1
Problems
- What is 98.6°F in degrees Celsius?
- What is 25.0°C in degrees Fahrenheit?
Solutions
- Using the first formula from above, we have: [latex]^{\circ}\text{C} = (98.6 – 32)\times \dfrac{5}{9} = 66.6 \times \dfrac{5}{9} = 37.0^{\circ}\text{C}[/latex]
- Using the second formula from above, we have: [latex]^{\circ}\text{F} = \left(25.0 \times \dfrac{9}{5}\right) + 32 = 45.0 + 32 = 77.0^{\circ}\text{F}[/latex]
Test Yourself
- Convert 0°F to degrees Celsius.
- Convert 212°C to degrees Fahrenheit.
Answers
-
-
- −17.8°C
- 414°F
-
The fundamental unit of temperature (another fundamental unit of science, bringing us to four) in SI is the kelvin (K). The Kelvin temperature scale (note that the name of the scale capitalises the word Kelvin, but the unit itself is lowercase) uses degrees that are the same size as the Celsius degree, but the numerical scale is shifted up by 273.15 units. That is, the conversion between the Kelvin and Celsius scales is as follows:
[latex]\begin{array}{rlrll} \text{K}&=&^{\circ}\text{C}&+&273.15 \\ ^{\circ}\text{C}&=&\text{K}&-&273.15 \\ \end{array}[/latex]
For most purposes, it is acceptable to use 273 instead of 273.15. Note that the Kelvin scale does not use the word degrees; a temperature of 295 K is spoken of as “two hundred ninety-five kelvins” and not “two hundred ninety-five degrees Kelvin.”
The reason that the Kelvin scale is defined this way is because there exists a minimum possible temperature called absolute zero. The Kelvin temperature scale is set so that 0 K is absolute zero, and the temperature is counted upward from there. Normal room temperature is about 295 K, as seen in the following example.
Example 1.4.2
Problem
If normal room temperature is 72.0°F, what is room temperature in degrees Celsius and kelvins?
Solution
First, we use the following formula to determine the temperature in degrees Celsius:
[latex]^{\circ}\text{C} = (72.0 – 32)\times \dfrac{5}{9} = 40.0 \times \dfrac{5}{9} = 22.2^{\circ}\text{C}[/latex]
Then, we use the appropriate formula above to determine the temperature in the Kelvin scale:
[latex]\text{K} = 22.2^{\circ}\text{C} + 273.15 = 295.4\text{ K}[/latex]
So, the room temperature is about 295 K.
Test Yourself
What is 98.6°F on the Kelvin scale?
Answer
310.2 K
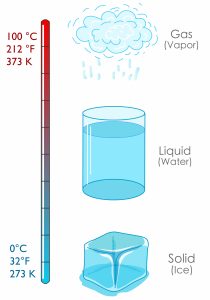
Figure 1.4.1 “Fahrenheit, Celsius, and Kelvin Temperatures” compares the three temperature scales. Absolute zero in each scale is −459°F, −273°C, and 0 K. Water freezes at 32°F, 0°C, and 273 K. 180°F equals 100°C, which equals 100 kelvins. Water boils at 212°F, 100°C, and 373 K. Note that science uses the Celsius and Kelvin scales almost exclusively; virtually no practising chemist expresses laboratory-measured temperatures with the Fahrenheit scale.
Density
Density is a physical property that is defined as a substance’s mass divided by its volume, as shown by the following equation:
[latex]\text{density} = \dfrac{\text{mass}}{\text{volume}}\text{ or } d = \dfrac{m}{V}[/latex]
In simpler terms, density describes how much mass is contained in a given volume. Objects with the same volume but different masses have different densities. This is because there is more or less mass packed into the same volume.
Density is usually a measured property of a substance, so its numerical value affects the significant figures in a calculation. Notice that density is defined in terms of two dissimilar units: mass and volume. That means that density overall has derived units, just like velocity. Common units for density include g/mL, g/cm3, g/L, kg/L, and even kg/m3. Densities for some common substances are listed in Table 1.4.1, “Densities of Some Common Substances”.
| Substance | Density (g/mL or g/cm3) |
|---|---|
| Water | 1.0 |
| Gold | 19.3 |
| Mercury | 13.6 |
| Air | 0.0012 |
| Cork | 0.22–0.26 |
| Aluminum | 2.7 |
| Iron | 7.87 |
Because of how it is defined, density can act as a conversion factor for switching between units of mass and volume. For example, suppose you have a sample of aluminum that has a volume of 7.88 cm3. How can you determine what mass of aluminum you have without measuring it? You can use the volume to calculate it. If you multiply the given volume by the known density (from Table 1.4.1 “Densities of Some Common Substances”), the volume units will cancel and leave you with mass units, telling you the mass of the sample is:
[latex]7.88\text{ cm}^3\times 2.7\text{ g/cm}^3=21\text{ g of aluminum}[/latex]
where we have limited our answer to two significant figures.
Example 1.4.3
Problem
What is the mass of 44.6 mL of mercury?
Solution
Use the density from Table 1.4 “Densities of Some Common Substances” as a conversion factor to go from volume to mass:
[latex]{44.6 mL × 13.6 g/mL = 607 g}[/latex]
The mass of the mercury is 607 g.
Test Yourself
What is the mass of 25.0 cm3 of iron?
Answer
197 g
Density can also be used as a conversion factor to convert mass to volume—but care must be taken. We have already demonstrated that the number that goes with density normally goes in the numerator when density is written as a fraction. Take the density of gold, for example:
[latex]d=19.3 \dfrac{\text{ g}}{\text{ mL}}=\dfrac{19.3\text{ g}}{1\text{ mL}}[/latex]
Although this was not previously pointed out, it can be assumed that there is a 1 in the denominator.
That is, the density value tells us that we have 19.3 grams for every 1 millilitre of volume, and the 1 is an exact number. When we want to use density to convert from mass to volume, the numerator and denominator of density need to be switched — in other words, we must take the reciprocal of the density. In so doing, we move not only the units but also the numbers, as can be seen below:
[latex]\dfrac{1}{d}=\dfrac{1\text{ mL}}{19.3\text{ g}}[/latex]
This reciprocal density is still a useful conversion factor, but now the mass unit will cancel, and the volume unit will be introduced. Thus, if we want to know the volume of 45.9 g of gold, we would set up the conversion as follows:
[latex]45.9\text{ g}\times \dfrac{1\text{ mL}}{19.3\text{ }\cancel{\text{g}}}=2.38\text{ mL}[/latex]
Note how the mass units cancel, leaving the volume unit, which is what we’re looking for.
Example 1.4.4
Problem
A cork stopper from a bottle of wine has a mass of 3.78 g. If the density of cork is 0.22 g/cm3, what is the volume of the cork?
Solution
To use density as a conversion factor, we need to take the reciprocal so that the mass unit of density is in the denominator. Taking the reciprocal, we find:
[latex]\dfrac{1}{d}=\dfrac{1\text{ cm}^3}{0.22\text{ g}}[/latex]
We can use this expression as the conversion factor. So:
[latex]3.78\cancel{\text{ g}}\times \dfrac{1\text{ cm}^3}{0.22\text{ }\cancel{\text{g}}}=17.2\text{ cm}^3[/latex]
Test Yourself
What is the volume of 3.78 g of gold?
Answer
0.196 cm3
Care must be taken with density as a conversion factor. Make sure the mass units are the same, or the volume units are the same before using density to convert to a different unit. Often, the unit of the given quantity must be first converted to the appropriate unit before applying density as a conversion factor.
Key Takeaways
- Chemistry uses the Celsius and Kelvin scales to express temperatures.
- A temperature on the Kelvin scale is the Celsius temperature plus 273.15.
- The minimum possible temperature is absolute zero and is assigned 0 K on the Kelvin scale.
- Density relates a substance’s mass and volume.
- Density can be used to calculate volume from a given mass or mass from a given volume.
Exercises
Media Attributions
- Kinetic energy is a form of energy associated with the motion of an object ↵

