5.2 Molar Mass and the Stoichiometry
Learning Objectives
- Apply the use of molar mass to allow for measurable quantities of atoms and molecules through weight.
- Understand how the molar mass of molecules is determined through the periodic table.
- Utilising stoichiometric coefficient, determine the masses of reactants needed to produce a desired amount of product, and vice versa.
In 2.5 Isotopes and Relative Abundance, we introduced the Dalton (Da) and the atomic mass unit (amu). These tell us the mass of individual atoms – which is roughly equal to the number of protons and neutrons.
Naturally, their small size makes it impractical for us to measure by the individual atom. As such, Avogadro's number was constructed with the mass of carbon-12 in mind (the same element used in the definition of Da and amu), allowing us to determine the amount of moles present in a material by weight. As such, practicing chemists hardly work with amu, but with Molar mass; the amount of grams required for 1 mole ([latex]gmol^{-1}[/latex]) of a substance. It is defined in such a way that it is equivalent in number to Daltons.
In the case of carbon-12, with an atomic mass of 12.01 Da, we can also read this as 12.01 grams needed to have 1 mole of carbon-12. For determining chemical equations with molar coefficients, this is extremely useful. We can now read our periodic table and determine the molar mass of any element (see Figure 5.2.1 and Table 5.2.1).
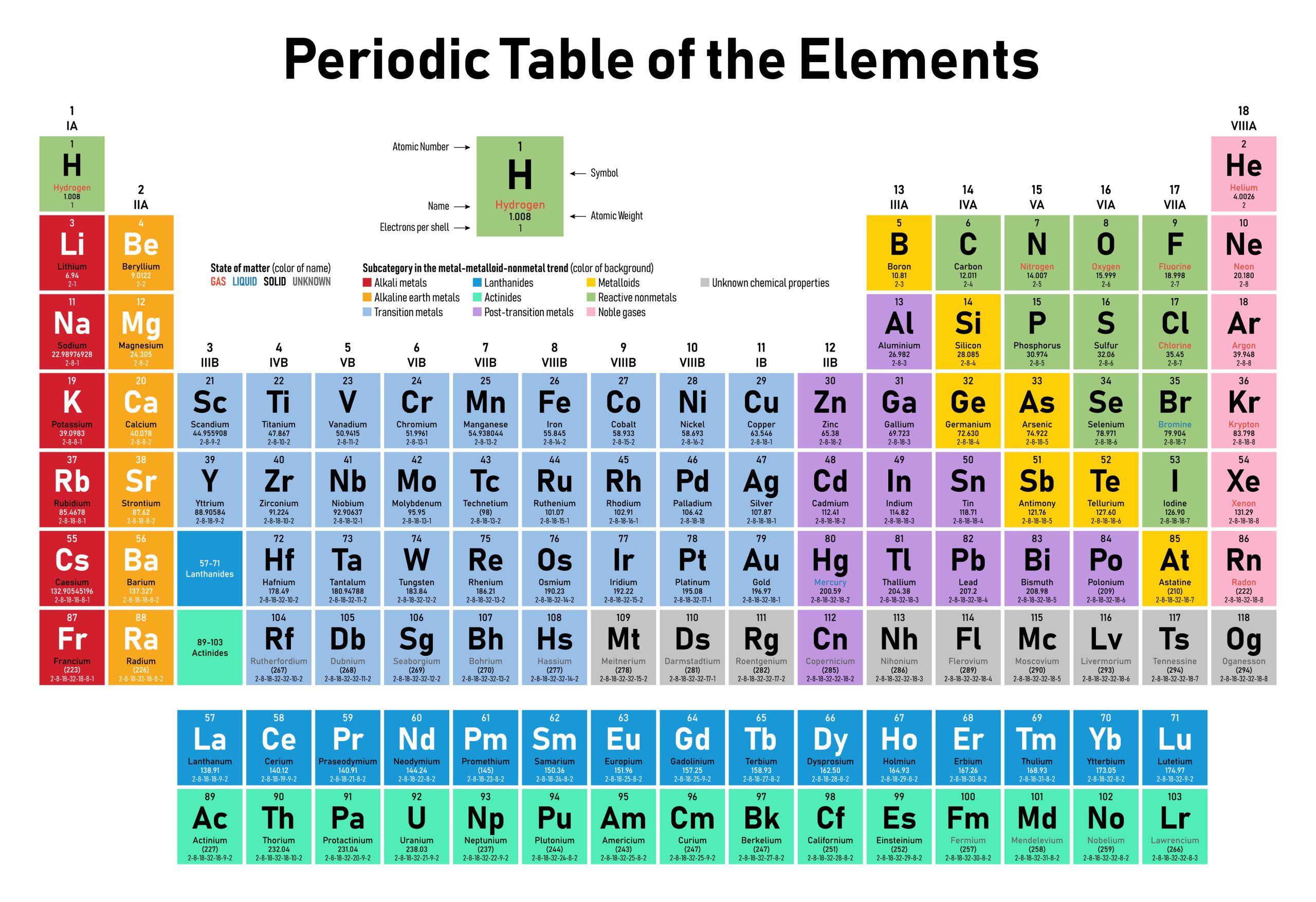
| Element | Molar Mass | Element | Molar Mass |
| [latex]\ce{H}[/latex] | [latex]1.01gmol^{-1}[/latex] | [latex]\ce{Na}[/latex] | [latex]22.99gmol^{-1}[/latex] |
| [latex]\ce{He}[/latex] | [latex]4.00gmol^{-1}[/latex] | [latex]\ce{Mg}[/latex] | [latex]24.31gmol^{-1}[/latex] |
| [latex]\ce{Li}[/latex] | [latex]6.94gmol^{-1}[/latex] | [latex]\ce{Al}[/latex] | [latex]26.98gmol^{-1}[/latex] |
| [latex]\ce{Be}[/latex] | [latex]9.01gmol^{-1}[/latex] | [latex]\ce{Si}[/latex] | [latex]28.09gmol^{-1}[/latex] |
| [latex]\ce{B}[/latex] | [latex]10.81gmol^{-1}[/latex] | [latex]\ce{P}[/latex] | [latex]30.97gmol^{-1}[/latex] |
| [latex]\ce{C}[/latex] | [latex]12.01gmol^{-1}[/latex] | [latex]\ce{S}[/latex] | [latex]32.06gmol^{-1}[/latex] |
| [latex]\ce{N}[/latex] | [latex]14.01gmol^{-1}[/latex] | [latex]\ce{Cl}[/latex] | [latex]35.45gmol^{-1}[/latex] |
| [latex]\ce{O}[/latex] | [latex]16.00gmol^{-1}[/latex] | [latex]\ce{Ar}[/latex] | [latex]39.95gmol^{-1}[/latex] |
| [latex]\ce{F}[/latex] | [latex]19.00gmol^{-1}[/latex] | [latex]\ce{K}[/latex] | [latex]39.10gmol^{-1}[/latex] |
| [latex]\ce{Ne}[/latex] | [latex]20.18gmol^{-1}[/latex] | [latex]\ce{Ca}[/latex] | [latex]40.08gmol^{-1}[/latex] |
Molar Mass of Compounds
To calculate the molar mass of a compound or molecule, we must add the molar masses of each atom found within it.
Example: What is the molar mass of Sodium Carbonate?
\textrm{The molar mass} & =\textrm{Sum of masses of atoms in a mole of the chemical species}\\
= & \left(2\times23.0\textrm{g}/\textrm{mol}\right)+12.0\textrm{g}/\textrm{mol}+\left(3\times16.0\textrm{g}/\textrm{mol}\right)\\
= & 106\textrm{g}/\textrm{mol}
\end{align*}\]
In sodium carbonate, 3 atoms of oxygen are needed to form only 1 molecule. We can directly relate this to the 3 moles of oxygen needed to form 1 mole of sodium carbonate.
The definition of molar mass creates an important relationship between the amount of substance (moles) and the mass of the substance (m): \[
n=\frac{m}{M}
\]
Where, [latex]M[/latex] is molar mass [latex]\left(\textrm{g}\textrm{mol}^{-1}\right)[/latex]
[latex]m[/latex] is the mass of the substance [latex]\left(\textrm{g}\right)[/latex]
[latex]n=[/latex] is the number of moles [latex]\left(\textrm{mol}\right)[/latex]
This is one of the most important formulas in chemistry! It allows us to determine the amount of moles of a substance present within a reaction through its mass.
Example: calculate the amount of silver present in 50.00g of silver. The molar mass of Ag is 107.87 grams per mole.
n & =\frac{m}{M}\\
n & =\frac{50.00\textrm{g}}{107.87\textrm{g}/\textrm{mol}}\\
n & =0.4635\textrm{mol}
\end{align*}\]
The Mole and Chemical Formulas
As we have learnt, chemical formulas indicate the number of atoms of each element present in a compound. For instance, in [latex]\ce{Na}_{2}\ce{CO}_{3}[/latex], one molecule of sodium carbonate contains two atoms of sodium, one atom of carbon and three atoms of oxygen. Similarly, chemical formulas can also indicate the number of moles of atoms of each type of element present in one mole of a compound. Let’s take the same example [latex]\ce{Na}_{2}\ce{CO}_{3}[/latex] again; this time, the chemical formula of sodium carbonate indicates that 2 moles of sodium, one mole of carbon and three moles of oxygen are present in one mole of sodium carbonate.
Example: The formula for aspirin is [latex]\ce{C}_{9}\ce{H}_{8}\ce{O}_{4}[/latex]. Calculate the mass of aspirin in grams present in [latex]0.65\textrm{mol}[/latex] of aspirin. The molar masses of [latex]\ce{C}[/latex], [latex]\ce{H}[/latex] and [latex]\ce{O}[/latex] are: [latex]\ce{C}=12.01\textrm{g}/\textrm{mol},\ce{H}=1.01\textrm{g}/\textrm{mol},\ce{O}=16.00\textrm{g}/\textrm{mol}[/latex].
\left(9\times12.01\textrm{g}/\textrm{mol}\right)+\left(8\times1.01\textrm{g}/\textrm{mol}\right)+\left(4\times16.00\textrm{g}/\textrm{mol}\right)=180.1\textrm{g}/\textrm{mol}
\] The next step is to rearrange the molar mass equation to make [latex]m[/latex] the subject: \[\begin{align*}
M & =\frac{m}{n}\\
m & =M\times n
\end{align*}\] The final step is to substitute the given values with units to the equation and solve the equation: \[\begin{align*}
m & =M\times n\\
m & =180.1\textrm{g}/\textrm{mol}\times0.65\textrm{mol}\\
m & =117\textrm{g}
\end{align*}\]
The relationship between mass, moles, and Avogadro’s number is a concept known as stoichiometry. Stoichiometry is present throughout chemistry, allowing us to determine the values of molecules and compounds through mathematical equations and calculations.
Stoichiometric Coefficient
In chemical equations, the stoichiometric coefficient is the number written immediately before the atoms, ions and molecules in a balanced chemical equation. These numbers indicate the ratio of any reactant or product that reacts or forms in a reaction.
For example, let’s consider the reaction between hydrogen gas and nitrogen gas to form ammonia. The balanced chemical equation can be written as follows: \[
3\ce{H}_{2}\left(g\right)+\ce{N}_{2}\left(g\right)\rightarrow2\ce{NH}_{3}\left(g\right)
\]
Stoichiometric coefficients are the numbers found in front of the reactants and products of our chemical equation. 3 and 2 are written in front of [latex]\ce{H_2}[/latex], and [latex]\ce{NH}_{3}[/latex] and are our coefficients. For components without a number, such as [latex]\ce{N_2}[/latex], we can treat this as a 1. Stoichiometric coefficients in this reaction show that three molecules of hydrogen gas react with one molecule of nitrogen gas to form two ammonia molecules.
The Molar Ratio and Chemical Equations
The stoichiometric coefficients in a balanced chemical equation can also be interpreted on the molar scale. For a general reaction such as:
[latex]\ce{aA + bB {\rightarrow} cC + dD}[/latex]
the number of moles of A divided by its stoichiometric coefficient a is equal to the number of moles of B divided by its stoichiometric coefficient b, etc., as shown in below equation:
[latex]{{\frac{Amol}{a}} = {\frac{Bmol}{b}} = {\frac{Cmol}{c}} = {\frac{Dmol}{d}}}[/latex]
Let’s consider the same example again: \[
3\ce{H}_{2}\left(g\right)+\ce{N}_{2}\left(g\right)\rightarrow2\ce{NH}_{3}\left(g\right)
\]
Based on the molar scale, we can say that three moles of hydrogen gas react with one mole of nitrogen gas to form two moles of ammonia gas. Molar scale interpretation relates to the quantities of substances involved in the reaction. Therefore, if we know the amount of one substance involved in the reaction, we can use the molar ratio to determine the amounts of others involved in the reaction.
Example: How many moles of ammonia gas can be produced from [latex]5\textrm{mol}[/latex] of hydrogen gas? \[3\ce{H}_{2}\left(g\right)+\ce{N}_{2}\left(g\right)\rightarrow2\ce{NH}_{3}\left(g\right)\]
We are asked to calculate the amount of ammonia and are given the moles of hydrogen and the balanced chemical equation for the reaction. We need to find out the molar ratio of hydrogen and ammonia to calculate the amount of ammonia. From the stoichiometric coefficients, we know that three moles of hydrogen produce two moles of ammonia. Therefore, the molar ratio of hydrogen gas to ammonia gas is [latex]3:2[/latex]. Thus, if we use [latex]5\textrm{mol}[/latex] of hydrogen gas, we can produce the following amount of ammonia gas: \[\begin{align*}
\frac{2\textrm{mol}\ce{NH}_{3}}{3\textrm{mol}\ce{H}_{2}} & \times5\textrm{mol}\ce{H}_{2}=7.5\textrm{mol}
\end{align*}\]
Example: How many molecules of SO3 are needed to react with 144 molecules of Fe2O3 given the balanced chemical equation [latex]\ce{Fe_{2}O_{3}(s) + 3SO_{3}(g) → Fe_{2}{(SO_{4})}_{3}?}[/latex]
Solution
We are asked to calculate the amount of sulphur trioxide and are given the moles of iron(III) oxide and the balanced chemical equation for the reaction. We need to find out the molar ratio of sulphur trioxide and iron(III) oxide. From the stoichiometric coefficients, we know that one mole of iron(III) oxide reacts with three moles of sulphur trioxide. Therefore, the molar ratio is [latex]1:3[/latex]. Thus, if we use [latex]144\textrm{mol}[/latex] of iron(III) oxide, we need the following amount of sulphur trioxide: \[\begin{align*}
\frac{3\textrm{mol}\ce{SO}_{3}}{1\textrm{mol}\ce{Fe}_{2}{(SO_{4})}_{3}} & \times144\textrm{mol}\ce{Fe}_{2}{(SO_{4})}_{3}=432\textrm{mol}
\end{align*}\]
We need 432 moles of SO3 to react with 144 moles of Fe2O3.
Mass Calculations
Now knowing how many moles are necessary of certain compounds, we can determine the weight of reactants needed to perform a reaction. Using the periodic table, we can calculate the molar masses of the reactants by adding individual atomic weights.
[latex]\ce{2AlCl_{3} + 3H_{2}O(ℓ) → Al_{2}O_{3} + 6HCl(g)}[/latex]
We will do this in two steps: convert the mass of AlCl3 to moles and then use the balanced chemical equation to find the number of moles of HCl formed. The molar mass of AlCl3 is 133.33 g/mol, which we have to invert to get the appropriate conversion factor:
[latex]n=\dfrac{m}{M}[/latex]
[latex]\dfrac{249\text{g}\ce{AlCl_{3}}}{133.33\text{gmol}^{-1}\ce{AlCl_{3}}} = 1.87\text{mol}[/latex]
[latex]1.87\cancel{\text{ mol }\ce{AlCl3}}\times \dfrac{6\text{ mol }\ce{HCl}}{2\cancel{\text{ mol }\ce{AlCl3}}}=5.61\text{ mol }\ce{HCl}[/latex]
Now, we can use this quantity to determine the number of moles of HCl that will form. From the balanced chemical equation, we construct a conversion factor between the number of moles of AlCl3 and the number of moles of HCl:
[latex]\dfrac{6\text{ mol }\ce{HCl}}{2\text{ mol }\ce{AlCl3}}[/latex]
Applying this conversion factor to the quantity of AlCl3, we get:
[latex]1.87\cancel{\text{ mol }\ce{AlCl3}}\times \dfrac{6\text{ mol }\ce{HCl}}{2\cancel{\text{ mol }\ce{AlCl3}}}=5.61\text{ mol }\ce{HCl}[/latex]
Alternatively, we could have done this in one line:
[latex]249\cancel{\text{ g }\ce{AlCl3}}\times \dfrac{1\cancel{\text{ mol }\ce{AlCl3}}}{133.33\cancel{\text{ g }\ce{AlCl3}}} \times \dfrac{6\text{ mol }\ce{HCl}}{2\cancel{\text{ mol }\ce{AlCl3}}} = 5.60\text{ mol }\ce{HCl}[/latex]
The last digit in our final answer is slightly different because of rounding differences, but the answer is essentially the same.
Stoichiometry is one of the fundamental concepts of chemical sciences. It is highly recommended that students get familiar and acquainted with the mathematical approaches employed in this and the next chapter, as future study will assume students’ knowledge in this area.
Key Takeaways
- Molar mass allows us to convert the mass of a substance present to the number of moles, using the atomic weight of elements from the periodic table.
- Molar mass of compounds is determined through adding the molar masses of individual elements.
- The moles and therefore mass of any products and reactants within a reaction can be determined through the stoichiometric coefficient.
Exercises
Media Attributions
Unit of atomic mass. 1 Da (or amu) is equal to 1/12th the mass of a carbon-12 atom.
One-twelfth of the mass of a carbon-12 atom.
Number of molecules within a mole of a substance; 6.02*10^23.
The mass of 1 mol of a substance in grams.
The relating of one chemical substance to another using a balanced chemical reaction.

