2.2 Electronic Configuration

Durga Dharmadana; Jack Benci; Matthew Millis; Joshua Muir; Jiawen Qu

2.2 Electronic Configuration

Learning Objectives

Learn how electrons are organised in atoms.
Represent the organisation of electrons by an electron/electronic configuration.
Understand the implications of paired and unpaired electrons within atoms.

Electron shells

Understanding how electrons arrange themselves within an atom is essential to predicting chemical bonding and interactions between atoms.

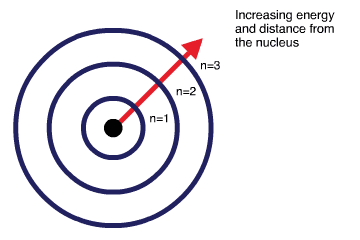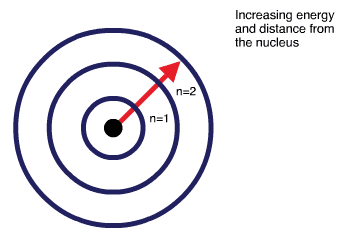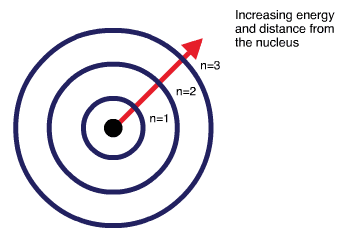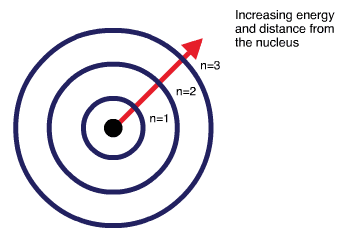
An arrow moving outwards from the centre of an atom, showing an increase of energy in orbitals when the distance to the nucleus increases. — Figure 2.2.1: Increasing energy and distance from the nucleus.

Space, where electrons move around the nucleus inside an atom, is divided into subspaces known as shells, subshells and orbitals.

The primary energy levels are called shells. The energy of the electron shells increases with distance from the nucleus. Therefore, the electrons closest to the nucleus have lower energy than the electrons located further away. Electron shells are named outward from the nucleus as [latex]1,2,3,4[/latex] and so on.

Electron shells have a maximum capacity of electrons which can occupy the entire shell at one time. This rule is known as the “2n Squared Rule”, where the [latex]Shell~Capacity = 2n^{2}[/latex], with [latex]n[/latex] equalling the shell number. As such, the first shell ([latex]n=1[/latex]) can hold 2 electrons, the second shell ([latex]n=2[/latex]) can hold 8 and so on.

While this rule is useful for understanding the capacity of a shell, it doesn’t predict the order in which electrons enter shells. Rather, electrons naturally occupy the lowest energy states possible. To understand that, we must analyse subshells and orbitals.

Electron subshell and orbitals

Within electron shells sit subshells. Subshells are labelled and ordered as [latex]s,p,d[/latex] and [latex]f[/latex]. Each subshell carries 2 electrons for each orbital present. An [latex]s[/latex] subshell has 1 orbital and can carry 2 electrons, a [latex]p[/latex] subshell has 3 orbitals and can carry 6 electrons, and so on. The number of subshells in a shell is equal to the shell number.

For instance, in the 3rd (n=3) electron shell, 3 subshells ([latex]s,p,d[/latex]) are present. If we add the amount of electrons within each subshell, we get 18 according to the 2n Squared Rule.

Shell number (n)	Subshells present	Number of orbitals	Number of electrons
1	[latex]s[/latex]	1	2

2	[latex]s[/latex]	1	2
	[latex]p[/latex]	3	6

3	[latex]s[/latex]	1	2
	[latex]p[/latex]	3	6
	[latex]d[/latex]	5	10


4	[latex]s[/latex]	1	2
	[latex]p[/latex]	3	6
	[latex]d[/latex]	5	10
	[latex]f[/latex]	7	14

Table 2.2.1: Electronic Shells, Subshells and Orbitals.

Schrödinger’s Model: Making Sense of Uncertainty.

The shapes of s, p, and d orbitals. The s orbital has a spherical shape, the p orbital has a dumbbell shape, and the d orbital has a cloverleaf shape. — Figure 2.2.2: The shapes of atomic orbitals. Image attribution: Atomic orbitals © extender_01 – stock.adobe.com

Orbitals are a product of the Schrödinger wave-mechanical model of electrons. Electrons in this model are not seen as physical particles but as energy waves surrounding the nucleus of an atom. Quantum mechanics tells us that it is impossible for us to know the location and velocity of where the electron is simultaneously. As such, the orbital is a prediction of where this energy can be likely found within an atom. For most of our investigation within this textbook, considering electrons as single particles simplifies explanations. Although we will bring up the orbital explanation if necessary.

Within an electron orbital, the two electrons enter spin states: one spin up, and the other spin down. Orbitals have distinct shapes, for instance. [latex]s[/latex] orbitals are spherical and [latex]p[/latex] orbitals are dumbbell shaped. This has further implications for predicting the bonding and stability of compounds. As orbitals are probability distributions of electrons, these can be added and subtracted when atoms bond. For double bonds, this causes the formation of pi (π) orbitals. This, however, is beyond the scope of what needs to be known in this chapter.

Predicting electron configurations

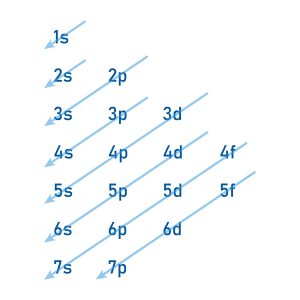
Illustration of electron configuration order in atomic orbitals, with diagonal arrows pointing downwards from the right, indicating the sequence from lower to higher energy levels is 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, and lastly 7p. — Figure 2.2.3: Aufbau Principle. Order to fill electron orbitals. Image attribution: Aufbau order of orbitals for feeding in electrons. Electron configuration. Aufbau principle. Filling orbitals in atom. Vector illustration isolated on white background. © SAMYA – stock.adobe.com

Electron subshells are filled in order of increasing energy. Figure 2.2.3 showcases the Aufbau principle: the order in which subshells fill with electrons depending on their energy. Beginning from the top left [latex]1s[/latex] shell, the order proceeds [latex]2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s[/latex] and so on. Note how the [latex]4s[/latex] subshell fills before the [latex]3d[/latex] subshell.

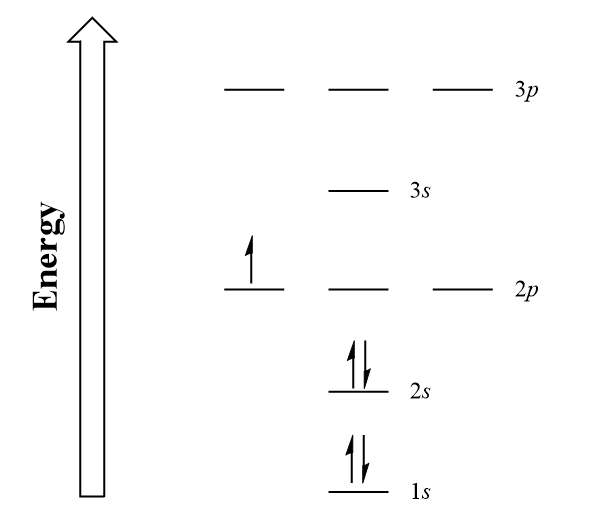
Electrons fill into orbitals of a subshell so that each orbital acquires one electron before any orbital acquires a second electron. All single electrons must have the same spin. Electron energy diagrams allow us to see this in action. Let us demonstrate the electron configuration of a standard boron atom, which has 5 electrons.

In Figure 2.2.4, we have drawn the first five electron subshells ([latex]1s[/latex] to [latex]3p[/latex]) in order of ascending energy levels with their respective orbitals. Note how the [latex]s[/latex] subshells have only 1 orbital present, whereas the [latex]p[/latex] subshells hold 3 each.

Let’s take our boron example. In a standard boron atom, we have 5 electrons to assign to orbitals. Beginning from the lowest energy subshells, two electrons (represented by up and down arrows) can be placed into the [latex]1s[/latex] subshell and two more into the [latex]2s[/latex] subshell. The leftover electron can be placed into one of the [latex]2p[/latex] orbitals. We can now describe the electronic composition of boron, being [latex]1s^{2}\,2s^{2}2p^{1}[/latex]: 2 electrons in [latex]1s[/latex], 2 in [latex]2s[/latex] and 1 in [latex]2p[/latex].

Subshells 1s, 2s, 2p, 3s and 3p are written from bottom to top, with underlines representing orbitals. s subshells have 1 underscore, while p subshells have 3. An up and a down arrow are found in both the 1s and 2s underscore, representing 4 electrons total. The 2p subshell has only 1 up arrow on one underscore. There are 5 arrows in total, representing the 5 electrons needed to be allocated. — Figure 2.2.4: Boron Electronic Energy Diagram Image attribution: “Generic Energy Diagram of Orbitals in a Multi-Electron Atom” by David W. Ball and Jessie A. Key © CC BY (Attribution). Transcript.

Moving across the periodic table, we can see how an additional electron is filled into 2p orbitals for each subsequent element (see Figure 2.2.5). For oxygen, we can finally pair up electrons with their opposite spin and fill one of the 2p orbitals.

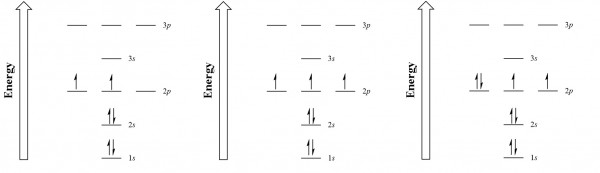
Carbon, Nitrogen and Oxygen Electronic Energy Diagrams. — Figure 2.2.5: Carbon (left-side), Nitrogen (middle) and Oxygen (right-side) Electronic Energy Diagrams. Image attribution: Chem&121: Introduction to Chemistry Copyright © 2023 by Lake Washington Institute of Technology is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License, Transcript.

Electronic configurations ^[1] are vital to understanding atomic bonding and the structure of the periodic table. As we will discuss in chapter 3.1 ‘The Octet Rule and Lewis Dot Diagrams’, valence electrons heavily dictate how many bonds an atom can achieve. Atoms naturally generate stable bonds by filling their outermost shell full of electrons. In the case of oxygen, two more electrons are needed in the [latex]2p[/latex] subshell to create a full 2nd shell — allowing electrons to form stable chemical bonds with two different atoms. For elements later down the periodic table, particularly the transition metals, ions that have extra or fewer electrons than normal may have the same amount of valence electrons due to the filling order. The periodic table, as we will see next chapter, can be divided up into subshell blocks, allowing us to predict chemical properties.

Table 2.2.2: The electron configuration of the first ten elements on the periodic table.
Element	Atomic number	Electron configuration
[latex]\ce{H}[/latex]	[latex]1[/latex]	[latex]1s^{1}[/latex]
[latex]\ce{He}[/latex]	[latex]2[/latex]	[latex]1s^{2}[/latex]
[latex]\ce{Li}[/latex]	[latex]3[/latex]	[latex]1s^{2}\,2s^{1}[/latex]
[latex]\ce{Be}[/latex]	[latex]4[/latex]	[latex]1s^{2}\,2s^{2}[/latex]
[latex]\ce{B}[/latex]	[latex]5[/latex]	[latex]1s^{2}\,2s^{2}2p^{1}[/latex]
[latex]\ce{C}[/latex]	[latex]6[/latex]	[latex]1s^{2}\,2s^{2}2p^{2}[/latex]
[latex]\ce{N}[/latex]	[latex]7[/latex]	[latex]1s^{2}\,2s^{2}2p^{3}[/latex]
[latex]\ce{O}[/latex]	[latex]8[/latex]	[latex]1s^{2}\,2s^{2}2p^{4}[/latex]
[latex]\ce{F}[/latex]	[latex]9[/latex]	[latex]1s^{2}\,2s^{2}2p^{5}[/latex]
[latex]\ce{Ne}[/latex]	[latex]10[/latex]	[latex]1s^{2}\,2s^{2}2p^{6}[/latex]

Key Takeaways

Electrons occupy orbitals found within subshells.
Subshells have an increasing number of orbitals as the shell number increases.
Electrons fill orbitals from the lowest energy upwards.
The electronic configuration is predicted using the Aufbau Principle, with the number of unpaired valence electrons vital to bonding.
Unless ionic or excited, the electron configuration of an element will always be the same.

Exercises