2.5 Isotopes and Relative Abundance
Learning Objectives
- Understand what an isotope is and how they differ from normal atoms.
- Express the masses of atoms with reference to relative abundance.
- Apply atomic masses to the mass of molecules.
Because matter is defined as anything that has mass and takes up space, it should not be surprising to learn that atoms and molecules have mass.
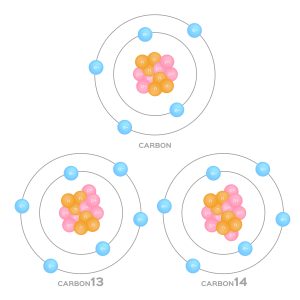
So far, we have assumed that all elements consist of the same mass. However, elements exist in a variety of isotopes — elements with the same amount of protons, but varying numbers of neutrons. Isotopes are named according to their element and atomic mass.
Individual atoms and molecules, however, are very small, and the masses of individual atoms and molecules are also very small. For macroscopic objects, we use units such as grams and kilograms to state their masses, but these units are much too big to comfortably describe the masses of individual atoms and molecules. As the mass of atoms is incredibly tiny (in the realm of [latex]0.000000000000000000000001 g[/latex] or [latex]1{\times}10^{-24}g[/latex]), the Dalton (Da) or atomic mass unit (amu) is used as a reference (both can be used interchangeably). Protons and neutrons weigh 1 amu each (the mass of electrons is negligible).
For instance, the 6 proton carbon atom has three stable, naturally occurring isotopes: carbon-12 ([latex]\ce{_{6}^{12}C}[/latex]), carbon-13 ([latex]\ce{_{6}^{13}C}[/latex]) and carbon-14 ([latex]\ce{_{6}^{14}C}[/latex]), weighing 12, 13 and 14 amu respectively. This extra weight is accounted for by the additional neutrons added. In chapter 5, we will discuss how Avogadro's number connects Daltons and atomic mass units to a more applicable measurement: grams per mole ([latex]g~mol^{-1}[/latex]).

Almost all elements exist as a mixture of isotopes. The atomic mass of an element is a weighted average of the masses of the isotopes that compose an element. A weighted average is found by multiplying each mass by its fractional occurrence (or relative abundance) and then adding all the products. The sum is the weighted average and serves as the formal atomic mass of the element. As such, the atomic masses listed on the periodic table take into account the relative abundance of each isotope. For instance, of all the carbon present, carbon-12 makes up 98.9% of it, while around 1% exists as carbon-13 and [latex]{1{\times}10^{-10}}[/latex] exists as carbon-14 [1]. To determine the atomic mass to list on the periodic table, we take the atomic masses of these isotopes and adjust them by their relative abundance, as seen in Table 2.5.1.
| Isotopes | Relative percentage abundance | Atomic mass (amu) |
|---|---|---|
| Carbon-12 | [latex]98.9[/latex] | [latex]12.00[/latex] |
| Carbon-13
Carbon-14 |
[latex]1.1[/latex]
[latex]{1{\times}10^{-10}}[/latex] |
[latex]13.00[/latex]
[latex]14.00[/latex] |
Carbon's atomic mass is calculated by multiplying the atomic mass of each isotope by its percentage abundance and then totalling the answers obtained for each isotope.
Carbon-12: [latex]\frac{98.9}{100}\times12.00\,amu=11.868\,amu\\[/latex]
Carbon-13: [latex]\frac{1.1}{100}\times13.00\,amu=0.143\,amu\\[/latex]
Carbon-14: [latex]\frac{1{\times}10^{-10}}{100}\times14.00\,amu={1.4{\times}10^{-11}}\,amu\\[/latex]
The atomic mass of carbon [latex]=11.868\,amu+0.143\,amu+{1.4{\times}10^{-11}}\,amu=12.011≈12.01\,amu[/latex]
Taking the weighted averages of masses, the atomic mass displayed for carbon on the periodic table is around 12.01 amu.
Virtually all elements exist as mixtures of isotopes, so atomic masses may vary significantly from whole numbers. Table 6.1 "Selected Atomic Masses of Some Elements" lists the atomic masses of some elements. The atomic masses in Table 6.1 are listed to three decimal places where possible, but in most cases, only one or two decimal places are needed. Note that many of the atomic masses, especially the larger ones, are not very close to whole numbers. This is, in part, the effect of an increasing number of isotopes as the atoms increase in size. (The record number is 10 isotopes for tin.)
| Element name | Atomic mass (amu) |
|---|---|
| Aluminum | 26.981 |
| Argon | 39.948 |
| Arsenic | 74.922 |
| Barium | 137.327 |
| Beryllium | 9.012 |
| Bismuth | 208.980 |
| Boron | 10.811 |
| Bromine | 79.904 |
| Calcium | 40.078 |
| Carbon | 12.011 |
| Chlorine | 35.453 |
| Cobalt | 58.933 |
| Copper | 63.546 |
| Fluorine | 18.998 |
| Gallium | 69.723 |
| Germanium | 72.64 |
| Gold | 196.967 |
| Helium | 4.003 |
| Hydrogen | 1.008 |
| Iodine | 126.904 |
| Iridium | 192.217 |
| Iron | 55.845 |
| Krypton | 83.798 |
| Lead | 207.2 |
| Lithium | 6.941 |
| Magnesium | 24.305 |
| Manganese | 54.938 |
| Mercury | 200.59 |
| Molybdenum | 95.94 |
| Neon | 20.180 |
| Nickel | 58.693 |
| Nitrogen | 14.007 |
| Oxygen | 15.999 |
| Palladium | 106.42 |
| Phosphorus | 30.974 |
| Platinum | 195.084 |
| Potassium | 39.098 |
| Rubidium | 85.468 |
| Scandium | 44.956 |
| Selenium | 78.96 |
| Silicon | 28.086 |
| Silver | 107.868 |
| Sodium | 22.990 |
| Strontium | 87.62 |
| Sulphur | 32.065 |
| Tantalum | 180.948 |
| Tin | 118.710 |
| Titanium | 47.867 |
| Tungsten | 183.84 |
| Uranium | 238.029 |
| Xenon | 131.293 |
| Zinc | 65.409 |
| Zirconium | 91.224 |
Now that we understand that atoms have mass, it is easy to extend the concept to the mass of molecules. The molecular mass is the sum of the masses of the atoms in a molecule. This may seem like a trivial extension of the concept, but it is important to count the number of each type of atom in the molecular formula. Also, although each atom in a molecule is a particular isotope, we use the weighted average, or atomic mass, for each atom in the molecule.
For example, if we were to determine the molecular mass of dinitrogen trioxide, N2O3, we would need to add the atomic mass of nitrogen two times with the atomic mass of oxygen three times:
[latex]\begin{array}{rrrrrl} &2\text{ N masses}&=&2\times 14.007\text{ amu}&=&28.014\text{ amu} \\ +&3\text{ O masses}&=&3\times 15.999\text{ amu}&=&47.997\text{ amu} \\ \hline &&&\text{total}&=&76.011\text{ amu}=\text{the molecular mass of N}_2\text{O}_3 \end{array}[/latex]
We would not be far off if we limited our numbers to one or even two decimal places.
Chemistry Is Everywhere: Sulphur Hexafluoride
On March 20, 1995, the Japanese terrorist group Aum Shinrikyo (Sanskrit for “Supreme Truth”) released some sarin gas in the Tokyo subway system; twelve people were killed, and thousands were injured. Sarin (molecular formula C4H10FPO2) is a nerve toxin that was first synthesised in 1938. It is regarded as one of the most deadly toxins known, estimated to be about 500 times more potent than cyanide. Scientists and engineers who study the spread of chemical weapons such as sarin would like to have a less dangerous chemical, ideally one that is nontoxic, so they are not at risk themselves.
Sulphur hexafluoride is used as a model compound for sarin. SF6 has a similar molecular mass (about 146 u) as sarin (about 140 u), so it has similar physical properties in the vapour phase. Sulphur hexafluoride is also very easy to accurately detect, even at low levels, and it is not a normal part of the atmosphere, so there is little potential for contamination from natural sources. Consequently, SF6 is also used as an aerial tracer for ventilation systems in buildings. It is nontoxic and very chemically inert, so workers do not have to take special precautions other than watching for asphyxiation.
Sulphur hexafluoride also has another interesting use: a spark suppressant in high-voltage electrical equipment. High-pressure SF6 gas is used in place of older oils that may have contaminants that are environmentally unfriendly. Additionally, being much denser than air, it can give a person a much lower voice — the opposite to helium! Compounds often have a variety of uses, with more always being discovered from the scientific community.
Key Takeaways
- Elements have a variety of isotopes: atoms with the same number of protons but different numbers of neutrons.
- Isotopes are named by their element and the number of subatomic particles in the nucleus. (Such as carbon-12, carbon-13, carbon-14).
- Atomic masses found on the periodic table are a weighted average of the relative abundance of all isotopes.
Exercises
Media Attributions
- isotope of carbon . 3 steps of carbon . vector © gritsalak - stock.adobe.com is licensed under a All Rights Reserved license
- parts of element on periodic table. carbon parts. chemical symbol atomic symbol and atomic mass © SAMYA - stock.adobe.com is licensed under a All Rights Reserved license
- cited from W.M. Haynes CRC Handbook of Chemistry 97th Edu. ↵
Atoms of the same element that have different numbers of neutrons.
A subatomic particle with a positive charge.
A subatomic particle with no charge.
The weighted average of the masses of the isotopes that compose an element.
Unit of atomic mass. 1 Da (or amu) is equal to 1/12th the mass of a carbon-12 atom.
One-twelfth of the mass of a carbon-12 atom.
Number of molecules within a mole of a substance; 6.02*10^23.
Ratio of different isotopes present in nature.

