7.4 Calorimetry and Heat Capacity
Learning Objectives
- Detail how calorimetry can be used to determine the amount of energy released in a chemical reaction.
- Discern the difference between constant-pressure (coffee cup) and constant-volume (bomb) calorimeters.
- Learn about specific and latent heat capacity and how they can be utilised in determining change in enthalpy.
Calorimetry
Determining the amount of energy within a reaction is an area of science known as calorimetry. Within calorimetry, a reaction is performed under known conditions. The enthalpy change will invoke an increase or decrease in the temperature of the environment (see Figure 7.4.1).
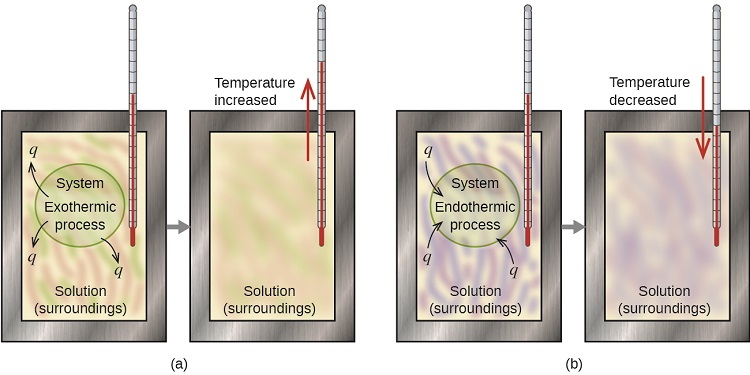
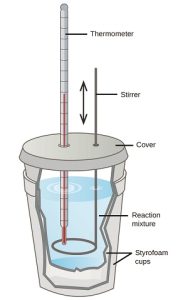
There are two types of calorimeters commonly used: constant pressure and constant volume, although they are more commonly referred to by less scientific names! "Coffee cup" calorimeters (constant pressure) involve the use of an insulated container to create a closed system. This can be easily achieved in science classrooms by stacking two polystyrene cups (see Figure 7.4.2). By filling the cup with a medium (commonly water), a reaction or process can then be facilitated, with the energy released or absorbed quantifiable through a change in temperature. In the case of sodium chloride salt being dissolved in water, the "enthalpy of dissolution" is positive - indicating an endothermic reaction. The temperature should, therefore, decrease. Due to the overall crudeness of this setup, energy readings will involve a degree of inaccuracy as energy seeps out from the container. Commercial options are available to alleviate these issues alongside providing more accurate electrical thermometers.

Bomb calorimeters (constant volume; see Figure 7.4.3) allow for the measurement of violent and energetic combustion reactions. A sealed "bomb" is loaded with the substance under investigation, with a source of ignition, generally an electrical spark, into an insulated container. The generated explosion will heat the water surrounding the bomb unit, allowing for energy release to be calculated. Bomb calorimeters are more accurate than their coffee cup counterparts but require calibration before use. Explosions are always exothermic processes, and so bomb calorimeters are generally useful in detecting increases in temperature.
Specific Heat Capacity
While it is easy for us to measure the temperature change of a substance, converting that figure demands that we know how much energy it takes to heat a given mass of a substance. Specific heat capacity is the amount of energy needed to heat 1 gram of a substance by one degree Celsius or Kelvin[1]. It is used in the following equation:\[
q=mc\Delta T
\]
Where, [latex]q[/latex] is the energy exerted or emitted [latex]\left(\textrm{J}\right)[/latex]
[latex]m[/latex] is the mass of the substance [latex]\left(\textrm{g}\right)[/latex]
[latex]c[/latex] is the specific heat capacity of the substance [latex]\left(\textrm{J}\textrm{K}^{-1}\textrm{g}^{-1}\right)[/latex] or [latex]\left(\textrm{J}\textrm{°C}^{-1}\textrm{g}^{-1}\right)[/latex]
[latex]\Delta T[/latex] is the temperature change of the substance [latex]\left(\textrm{K}\right)[/latex] or [latex]\left(\textrm{°C}\right)[/latex]
While different substances will have different heat capacities — commonly utilised environmental mediums have been well-documented in scientific literature. Water is the most common substance, thanks to its availability and relatively high specific heat capacity (owing to its strong hydrogen bonding). It is recommended to learn the heat capacity of water by memory. For any other substances, capacities will be given within the question.
| Substance | c ([latex]JK^{-1}g^{-1}[/latex]) |
|---|---|
| water | 4.184 |
| steam | 1.864 |
| ethanol | 2.376 |
| air | 1.007 |
| iron | 0.449 |
| gold | 0.129 |
| helium | 5.193 |
You may be wondering as to how these units were initially discovered. After all, to determine how much energy is needed to heat a substance, we would have needed to know how much energy was being provided initially. So, what came first?
As you may have noticed, the word 'calorimetry' derives from the energy unit 'calorie'. Within the early days of this science, 1 calorie was understood to be the energy needed to heat 1 gram of water by 1 degree Celsius. From this, the heat capacities of other substances were determined. Since then, the global scientific community has pushed for the standardisation of units and measurements across fields. As such, outside of medical health and nutritional studies, scientists instead utilise joules (J) as the preferred energy unit. To convert, utilise the following relationship:
[latex]1~cal = 4.184~J[/latex]
This book will continue to utilise the joule when referring to energy. We can all agree however 'Joulrimetry' definitely doesn't run off the tongue as well!
Example: A calorimeter filled with 500g of water is heated from 298K to 344K. How much energy has the system absorbed?
From the question, we can determine the following quantities:
[latex]m=500g[/latex]
[latex]\Delta T= 344-298= 46K[/latex]
From literature, we know that the specific heat capacity of water [latex]c[/latex] will be [latex]4.184JK^{-1}g^{-1}[/latex]. We can now utilise these values in the following equation:
[latex]q=mc\Delta T[/latex]
[latex]q = (500g)\times(4.184JK^{-1}g^{-1})\times(46K)[/latex]
[latex]q = 96232J[/latex] (or [latex]96.232 kJ[/latex])
This process saw 96.232 kJ of energy absorbed by the system.
Latent Heat Capacity
Whereas specific heat details the amount of energy needed to heat a substance, latent heat capacity quantifies the amount of energy needed to induce a state change within a substance. It utilises the following equation:
\[
q=mL
\]
Where, [latex]q[/latex] is the energy exerted or emitted [latex]\left(\textrm{J}\right)[/latex]
[latex]m[/latex] is the mass of the substance [latex]\left(\textrm{g}\right)[/latex]
[latex]L[/latex] is the latent heat capacity of the substance of the transformation taking place [latex]\left(\textrm{J}\textrm{g}^{-1}\right)[/latex] or [latex]\left(\textrm{J}\textrm{g}^{-1}\right)[/latex]
The type of latent heat described depends on the transformation taking place:
- Latent heat of fusion — the amount of energy required or released during solid/liquid conversion.
- Latent heat of vaporisation — the amount of energy required or released during liquid/gas conversion.
- Latent heat of sublimation — the amount of energy required or released during solid/gas conversion.
| Substance | c ([latex]Jmol^{-1}[/latex]) |
|---|---|
| Latent heat of fusion (Solid/Liquid) |
6010 |
| Latent heat of vaporisation (Liquid/Gas) |
2256 |
Figure 7.4.4 shows the change in temperature of a substance as heat is applied. Note that during a change in state, such as in the freezing or melting process, the temperature doesn't change — energy is focused into overcoming intermolecular forces holding molecules together. Additionally, the gradients between the state changes may also be different, as the different states of matter within a substance will have different specific heat capacities.
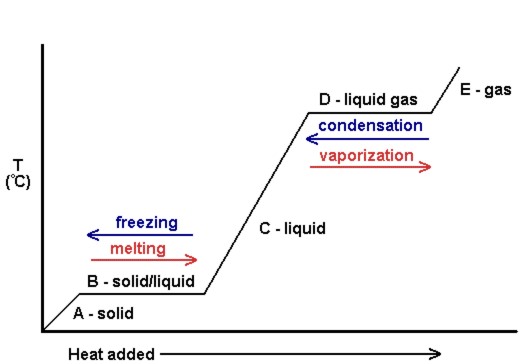
This principle of temperature not rising when a state transformation takes place is commonly used within chemistry for extractions and purifications but also in many other real-world applications. For instance, rice cookers use this to know when to automatically turn off. If the temperature is measured to be above 100°C, all of the water must be evaporated, as the rice and water mixture wouldn't be able to rise further if water was still present. That must mean the rice is fully cooked!
Key Takeaways
- Calorimeters measure the change in enthalpy of a given reaction, through detecting a change in temperature of a liquid medium.
- Two main types of calorimeters exist: constant-pressure (coffee-cup) and constant-volume (bomb) calorimeters.
- Specific heat capacity is the amount of energy needed to increase 1 gram of a substance by 1 degree.
- Latent heat capacity is the amount of energy needed to change the state of 1 gram of a substance.
Exercises
Media Attributions
- Calorimetry © Manjusha T Saraswathiamma is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Coffee Cup Calorimeter © Manjusha T Saraswathiamma is licensed under a CC BY-NC-SA (Attribution NonCommercial ShareAlike) license
- Bomb calorimeter vector illustration. Labeled educational explain scheme. © VectorMine - stock.adobe.com
- Kelvin and Celsius can be used interchangeably, as we are measuring the change in temperature, not the absolute value. Both increase at the same rate ↵
The enthalpy change of a substance being dissolved.
The proportionality constant between heat, mass, and temperature change; also called specific heat.

